Option Greeks Explained
Delta, Vega, Theta, and Gamma – No…Those aren’t the names of a trading fraternity. These streaming numbers on your options chart aren’t random; they are important symbols known as the Greeks. These formulas are essential to all option traders, whether they realize it or not. “The Greek alphabet measures an option contracts price, time, and implied volatility.” Greek options explained is a high-level overview of option Geeks and the role they play for options traders.
Before you feel overwhelmed, rest assured that you won’t have to learn an entirely new language. However, there are four specific Greek symbols that you will need to remember, as they are essential to every option contract. The Greeks are critical as they help traders recognize the risk associated with any options trade. A basic understanding of the Greeks will help a trader become more knowledgeable and make better trading decisions.
Risks and Opportunities: Greek Options Explained
An option is a contract that gives you the right to buy or sell a financial product at an agreed-upon price, known as the strike price, for a specific period of time. The option’s value is “derived” from the underlying asset or stock. When you trade options contracts, you are buying or selling a contract that represents the potential of the underlying stock rather than the stock itself. Typical stock option contracts cover 100 shares of an underlying stock. Traders use the Greeks to measure the external variables that move an option contract’s price.
There are four primary Greek risk measurements known as an option Delta, Theta, Vega, and, Gamma. If you’ve been in the Simpler Trading Options Room, you’ll hear the Greeks referred to regularly.
This short introduction to options Greeks will allow us to accurately assess what might happen to the price of an option when the market moves:
- Delta – Considered the most important Greek measurement, can help gauge the likelihood an option will expire in the money (ITM) or out of the money (OTM). This means the strike price is below (for calls) or above (for puts) the underlying stock’s market price.
- Theta – measures how much value an option contract will lose each day the contract approaches its expiration date.
- Vega – measures how sensitive an option is in relation to large price swings in the underlying stock or asset.
- Gamma – measures the rate of change in delta in relation to movement in the underlying stock or asset.
- Rho – While not a primary formula, Rho measures the effect of interest rate changes on an option. As Rho does not significantly impact options trades, we don’t use this one often, but it still deserves mention.
As we consider how options prices are predicted, traders use the Greeks to look for specific results from their setups.
Delta Measurement of Price
First, we meet Delta. This Greek measures how much an options contract value changes in relation to a $1 dollar movement in the underlying stock or index price.
A Delta of 0.40 means the option’s price will theoretically move $0.40 for every $1 change in the underlying stock or index price. If the underlying stock’s price moves up OR down, the options contract price will increase or decrease accordingly.
We can also use Delta to predict whether an option will expire in the money (ITM). With a Delta of 0.40, the option has about a 40% chance of being ITM at its expiration.
Because options contracts are leveraged derivatives, they control the movement of 100 shares of the underlying stock. With a Delta of 0.40, should the underlying share price go up by $1, my options contract value will go up $40. Delta measurements of Call and Puts react differently.
Call options:
- Call options have a positive Delta range from 0.00 to 1.00 – with 0.00 reflecting far OTM options and 1.00 reflecting deep ITM options.
- At the money (ATM), options have a delta of around 0.50. This means that when the stock increases by $1, the option’s market price rises by 50 cents.
Put options:
- The Delta of put options can reach values between –1.00 (with deep ITM puts) and 0.00 (with far OTM puts).
- At the money (ATM), put options have a delta around –0.50. When the underlying stock decreases by $1, the put option’s value rises by 50 cents (the inverse of call options). In addition, think of a 50 / 50 chance of being ITM or OTM.
Gamma Measures Rate of Change
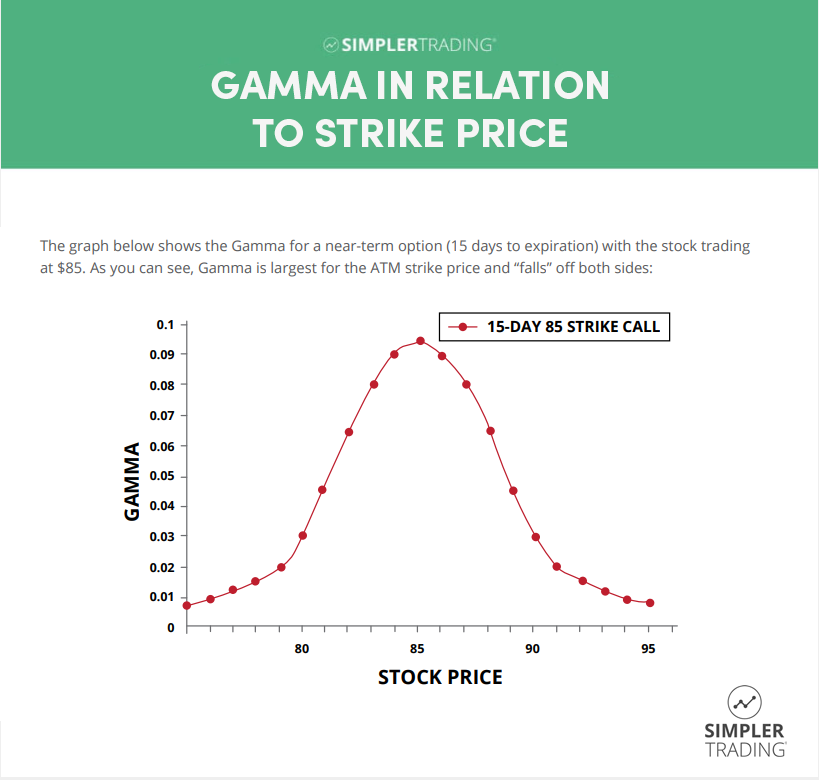
The Greek symbol known as Gamma shows up to measure Delta’s rate of change over time. A key takeaway is that Gamma serves as a velocity gauge for the potential change in Delta. Gamma measures the rate of change in an option’s Delta per 1-point move in the underlying stock’s price. Should the underlying stock move $1 and the option moves $.40 along with it, the option’s Delta is no longer 0.40 – as this $1 move would mean the call option is now even deeper ITM. So, Delta should move even closer to 1.00.
Assuming the resulting Delta is now 0.55. The change in Delta from 0.40 to 0.55 is 0.15 is the option’s Gamma. Gamma is typically at its highest when the price of the stock is closest to the option’s strike price (ATM). As an options contract moves further ITM or OTM, the Gamma will decrease accordingly.
Theta Time
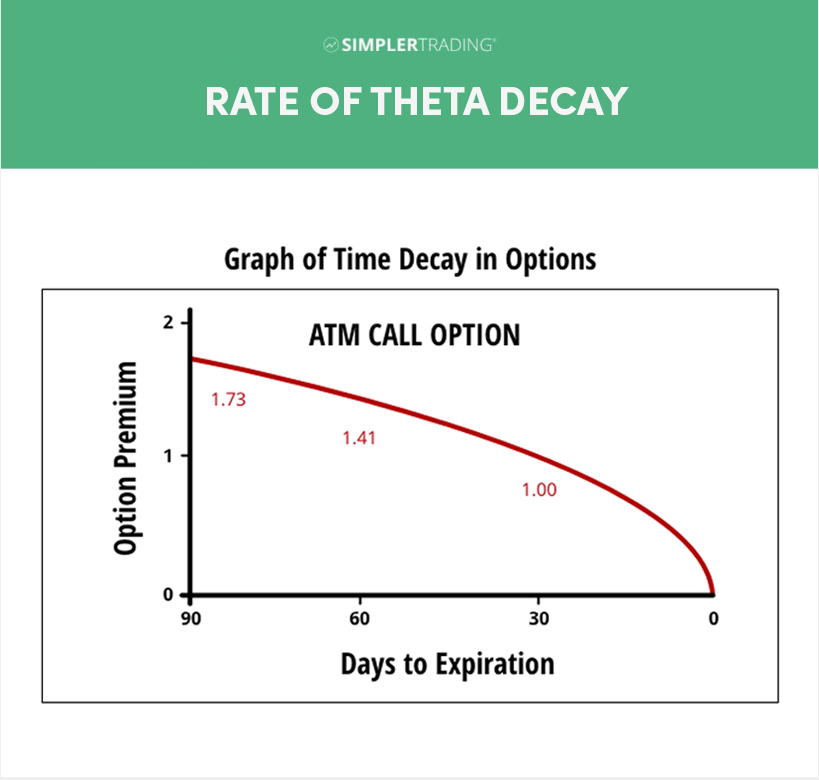
An easy way to think about theta is time. Theta = Time. Theta measures how much the price of an option should decrease each day as the option nears expiration – should all other factors stay the same. We also refer to price erosion over time as time decay. Time decay, or theta decay, works against buyers, but it works for sellers.
Time-value erosion tells us that the price erosion of at-the-money (ATM), just slightly out-of-the-money, and in-the-money options, tend to increase as expiration approaches. Although, far out-of-the-money (OOTM) options tend to decrease as expiration draws near.
Vega Volatility
The early traders took liberty when naming the measure of implied volatility – as Vega is not actually a Greek letter. Vega measures the rate of change in an option’s price per one-percentage-point change in the implied volatility of the stock. Vega tells us how much an option’s price should move when the volatility of the stock increases or decreases.
Volatility is one of the most critical factors affecting the value of options. The further out an expiration is, the higher the Vega will be.
Puts and calls are strongly reactive to changes in Vega. Traders should consider buying options when Vega is below “normal” levels and selling options when Vega is above “normal” levels. This can be determined by comparing the historical volatility to the implied volatility. Implied volatility forecasts how volatile an underlying stock is expected to be in the future. Historical volatility can give us some insight into the forecast of a stock’s future moves. However, the implied volatility is based on other factors such as earnings announcements, political conditions, or even new products to the market.
Option Greeks Explained – Master the Fundamentals With Bruce
Options traders know that understanding the Greeks is imperative to protecting yourself against the risks associated with options trading. Bruce Marshall, Director of Options & Income Trading at Simpler Trading, who has traded both at the retail and institutional level, teaches traders the real-world way to use Greeks. Bruce gives traders full exposure to the Greeks from a practical standpoint. He teaches traders to recognize risk in trades and the overall portfolio.
Bruce’s method of teaching will help you to understand how the Greek may affect a potential trade before you enter the order.
He teaches trade setups and also provides detailed examples of trades and how they were affected by the Greeks.
Bruce’s trading style allows him to enter trades with larger time frames that are often more forgiving. His goal as a trader is to produce income by utilizing option spreads that do not require him to sit in front of his trading station all day, putting out fires. By understanding the Greeks, Bruce is able to consistently produce income as a trader by taking high-probability setups by selling premiums and letting Theta-Decay work in his favor.
If you have been searching for a less stressful, higher probability trading strategy, working with Bruce Marshall may be your golden ticket.
Join our Free Trading Room today to watch Bruce and other successful traders execute live trades. Our traders provide a thorough technical analysis of stocks and are happy to answer your questions. Simpler Trading pioneered the live trading room. As industry leaders, our goal is to help traders like you become financially independent.
Sign up today and never trade alone again.
FAQs on the Option Greeks Explained
A: An option is a contract that gives you the right to buy or sell a financial product at an agreed-upon price for a specific period. Options are available on numerous financial products, including equities, indices, and ETFs. Options are called “derivatives” because the value of the option is “derived” from the underlying asset. When you buy or sell options contracts, you are trading the potential, or obligation, to buy or sell the underlying stock. Owning an option, in and of itself, does not impart ownership in the underlying security, nor does it entitle the holder to any dividend payments.
A: Options traders look to Vega to determine how volatile a stock will be at any given time. While difficult to measure, implied volatility, which is often provided on trading platforms, can give us a sense of what assumptions market makers are using to determine their bid and ask prices. By comparing the stock’s implied volatility to the historical volatility, we can sometimes get a sense of whether an option is priced higher or lower than normal.
Traders often see lower-than-normal implied volatilities are more favorable for option buyers because volatility often reverts to its mean over time.
A: Let’s say the current share price of a stock is $20. What a delta of 0.63 means – in terms of contracts that are 100 shares – is this is going to be per share. That means, if the share price were to go up, then the share price increase of $1 means the options premium will be affected by the Delta of 0.63. So, that means that the option price will go up 63 cents.
This works in reverse, as well; if the share price went down to $19, then the premium would go down 63 cents. For calls, Delta is going to be anywhere between 0.00 and 1.00. The further we are in the money away from the share price, the closer to a delta of 1.00 we get.


